1.0 Introduction

The need to know the impedance of a piezoceramic element in use as an actuator stems primarily from the desire to match impedance between the driving circuit, and the actuator. In addition, impedance measurements yield information about the efficiency of the actuator, by allowing the measurement of electrical and mechanical losses. This second benefit of impedance measurement leads to the question of the feasibility of utilizing impedance as a measure of transducer health. This report will touch upon the difficulties inherent in making the connection between electrical Q (measured electrical quality factor) and actuator damage such as debonding and cracking. Additionally, this report will show the relationship between actuator resonance, and equivalent electrical resonance. Claims by Uchino [1] regarding the relationship between natural modes of the actuator, and resonance and anti-resonance of the equivalent circuit will also be addressed.

2.0 One-Dimensional Electro-Mechanical Model

Figure 1 One- dimensional actuator using the T- effect under z-direction poling.

A simple rod or extensional beam model is shown in Fig. 1. Assumptions: (i) the beam is assumed to be thin in the thickness direction (x3-direction), and width direction (x2-direction) as compared to its length, L, in the x1-direction. (ii) Further, it is assumed to be thinly electroded on its top and bottom (x3) surfaces, and to (iii) exhibit negligible deformation in either the x2 or x3-directions. Hence, it is assumed to be infinitely stiff in these directions as compared with the x1-direction. The popularity [2,3, 4] of such a simple approach will become apparent in the following analysis.

Under the above assumptions, the governing equations may be shown to be

, (1)

, (2)

and , (3)

where the parameters and variables are defined in Table 1.

Table 1 Variable and parameter list

       Stress in x1 direction [N/m2]               
       Displacement in x1 direction [m]            
               Strain in x1 direction =           
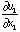
          Electric field in x3 direction [V/m]     
        Flux density or electric displacement in   
                x3 direction [Coulombs/m2]          
                 Density of PZT [kg/m3]            
       Lengthwise-clamped dielectric constant in   
          x3 direction [Farads/m, Coulombs/v-m]     
         Compliance in x1 direction in constant    
                  electric field [m2/N]             
       Transverse piezoelectric coefficient        
        [Coulombs/N, m/V]                           

Equations (1) through (3), represent the electromechanical governing equations for this system under the assumptions of (1) quasi-static electric field [3.5], and (2) symmetric constitutive tensor reduction [5]. Assumption (1) implies that the characteristic wave length of mechanical vibration is much shorter than the electric field wave length in PZT, or that the propagation speed of sound in PZT is much slower than the speed of light. This is a valid assumption. Assumption (2) is equally valid under the assumption of the symmetric stress tensor [5].

The collateral mechanical boundary condition equations are given by:

, (4)

, (5)

and the collateral electrical conditions are:

, (6)

Hence,

. (7)

In the above equations, and henceforth, the subscripts will be dropped when no ambiguity will result. In addition, from the definition of strain in Table 1, and letting u = u1, we have

, (8)

and, from the definition of compliance, we have

, (9)

where Y1 is the Young's modulus of the PZT in the x1 direction (neglecting the effect of the electrodes).

Using the definitions given in Table 1, and Equations (6) through (9), Equation (2) becomes

, (10)

and Equation (3) becomes

. (11)

Hence, Equation (1) becomes

,

or

, (12)

where is the speed of sound in the PZT. The steady-state solution of equation (12), assuming harmonic electrical excitation, is given by

, (13)

where, x = x1. Substitution of (13) into (4) yields A = 0. Substitution of equations (13) and (10) into (5) yields , assuming . Hence, the displacement of the PZT actuator in the x = x1 direction is given by

, (14)

where . Substitution of (14) into (11) yields

, (15)

where . Thus, the current flowing from the electrodes is given by

. (16)

Substitution of (15) into (16) yields

. (17)

Thus, we can compute the electrical impedance of the actuator as seen by a driving circuit,

. (18)

Equivalently, the admittance is given by

. (19)

3.0 Electrical Admittance - Limiting Cases

Equation (19) permits two limiting cases: (1) 0, and (2) [[infinity]]. 0 occurs for [[omega]] = 0, (the trivial case) and when

,

or

, (20)

where [[omega]]A is termed the "anti-resonance" frequency. Equation (20) describes the so-called anti-resonance condition for this system. It is clear that there are an infinite number of such anti-resonance frequencies. Equation (20) is plotted versus frequency in Figure 2 for the parameters given in Table 2.

Figure 2 Plot of equation 20 versus [[omega]]

The [[omega]]A-axis crossings represent anti-resonance frequencies in radians/s, and the peaks represent resonance frequencies. Clearly, the anti-resonance behavior is dominated by the poles of the tangent function. This is because the linear part (in [[omega]]A) of equation (20) has a very small coefficient ( ) given the parameters in Table 2. Hence, for lower frequencies ([[omega]] <= 100,000 rad/s), anti-resonance is governed by

, (21)

or , (22)

for n = 0, 1, 2,... In fact, for this example, Equation (20) yields [[omega]]A1 = 52,963 rad/s (exact), and Equation (22) yields [[omega]]A1 = 52,967 rad/s.

Table 2 Example parameter values for PZT 2 [5]

 Y1                 1.35X1012 N/m2  
[[eps     2.2997x10-9 Coulombs/V-m  
ilon]                               
  ]                                 
 d31          -60x10-12 Coulombs/N  
[[rho                   7700 kg/m3  
 ]]                                 
  c                       4215 m/s  
  h                         0.05 m  
  L                         0.25 m  
  b                          0.1 m  

, (23)

which occurs when , (24)

Hence, the electrical resonance corresponds to the mechanical resonance in this case. This is because for the transverse effect (T-effect), there is no electromechanical coupling in the free vibration problem. It should be noted that the discontinuity in the tangent function is a mathematical artifact, and is not observed in nature. The phase of an oscillating system with respect to a given excitation is continuous and unique to within +/- [[pi]]. Hence, a better representation of the resonance condition would plot versus frequency, but former case was plotted to make it easier to graphically locate [[omega]]R in Figure 2.

4.0 Mechanical Response at Resonance and Anti-Resonance - Wavelength Perspective

Another way to view the resonance and anti-resonance conditions is given by the wavelength of vibration in the PZT given by

. (25)

Substituting Equations (22) and (24) into (25) yields wavelength of vibration at anti-resonance and resonance respectively

, (26)

and

, (27)

where n is the mode of vibration. From Equations (22) through (27) we find that the frequency and wavelength relationship between resonance and anti-resonance is given by

. (28)

We see that for the example system, [[kappa]]n < 1 which implies that the resonance frequency is always lower than the anti-resonance frequencyin this case. Conversely, the resonance wavelength is always longer than the anti-resonance wavelength in this example. Here, the first resonance condition occurs when the frequency of excitation produces vibration with wavelength 4L. In other words, the length of the PZT bar is one-quarter the length of the sound wave in the actuator. Similarly, the first anti-resonance wavelength occurs when [[lambda]] = L/2. This relationship is represented in Figure 3, where uR(x) and uA(x) represent the displacement amplitudes at resonance and anti-resonance respectively. The dashed bars represent extension of the PZT to four times its length. It can be seen from Figure 3 that the first resonance produces a maximum displacement at x = L. The anti-resonance amplitude is shown smaller than the resonance amplitude which would actually be infinite in the absence of mechanical damping or losses. This can be seen from Equations (14), (24) and (25). The dashed waveforms represent strain at the first resonance and anti-resonance. The first anti-resonance produces an equal amount of compression and extension, thereby canceling out the resultant piezoelectrically induced charges. The first resonance strain, however, produces all extension or all compression which creates all positive or all negative charges in the PZT. It is the transport of these positive and negative charges between the two electrodes which enables current to flow within the driving circuit. Figure 3 reveals where the notion, due to Uchino [1], of modes which preserve PZT actuator volume and those which do not. The integrated strain in the anti-resonance case yields zero net extension, and hence, zero net volume change in the actuator.

Figure 3 First resonance and anti-resonance displacement and strain wave-forms.

4.1 Invariant and non-invariant volume modes

Comparison of Equations (26) and (27) reveals that anti-resonance modes preserve the volume of one-dimensional T-effect piezoelectric actuators such as the one described here when n is even. In other words, for even anti-resonance modes, there is an equal amount of compressive and extensional regions within the actuator. This is because anti-resonance wavelengths always occur in integral fractions of the actuator length for even n - i.e. L/[[lambda]]A is an integer for even n. The resonance wavelengths, however, always create an imbalance between compressive and extensional strains because L/[[lambda]]R is never an integer. What this means electrically is that in the anti-resonance case, an even number of positive and negative charges are produced by the symmetric strain, and since these can flow freely on the electroded surfaces, they cancel each other out, and, ideally, no current can flow. For odd anti-resonance modes, a net unbalance in positive and negative strain is produced, but the strain amplitudes are so much smaller than in the resonance case that very little current is produced. The converse is true in the resonance case, where there is always an imbalance in positive and negative charge and high-amplitude strains, so there is always a potential to drive current.

5.0 Equivalent Circuits

Equivalent circuits are used in the description of piezoelectric systems for simplicity, and to determine the impedance match for driving circuits. Equations (18) and (19) give the impedance and admittance of the actuator directly, but are not suitable for representation via equivalent circuit due to the nonlinear, , term. The common treatment for this difficulty is to limit attention to mechanical resonance or anti-resonance - i.e. to values of [[omega]] where Accordingly, the tangent function may be expanded near a resonance via the Mittag-Leffler theorem [5] which is given by

, (for odd n) (29)

where , (for odd n) (30)

and , (for odd n) (31)

at resonance. Application of Equations (29) through (31) on Equation (19) yields

, (32)

where , (33)

, (34)

, (35)

and where

, (36)

, (37)

and . (38)

Equations (32) through (38) describe the admittance of an equivalent parallel circuit of the form shown in Figure 4. Here the so-called motional current is given by im(t), and the so-called clamped current is given by i0(t). The clamped capacitance C0 is the capacitance measured under constant voltage and where the actuator is fixed or clamped.

Figure 4 Equivalent circuit for resonance condition.

The equivalent admittance for the circuit shown in Figure 4 is given by

. (39)

Hence, the resonance frequency is given by

. (40)

Equation (40) predicts the first resonance frequency exactly (26,481 rad/s), but the predicted anti-resonance frequency given by

, (41)

is invalid. This should not be surprising, since the equivalent circuit parameter values were determined from an expansion of the tangent function around a resonance frequency. However, Ikeda [5] offers a correction (with very little explanation) where C0 is replaced by given by

. (42)

Substitution of equation (42) into (41) in place of C0 yields a predicted anti-resonance frequency for the example system (Table 2) which is approximately 12% higher than the value given by Equation (22) for n = 1 (59, 214 versus 52,963 rad/s).

6.0 Summary

This report has addressed several issues of interest from the perspective of traveling wave motor development. The simplest possible continuous mechanical model has been used to reveal the salient physics of the electromechanics of piezoceramic actuators. This study is far from complete, but should expose the relevant issues. The following issues have been developed here:

1. The analysis of asimple T-effect piezo-actuator has been presented to explain the physics of electromechanical resonance and anti-resonance.

2. The question of "volume preserving" modes has been addressed and explained.

3. An equivalent electrical circuit has been developed, and the limitations thereof have been explained.

4. An example (Table 2) has been worked out, and all of the equations presented have been verified.

The example derived here neglects both dielectric and mechanical losses. These may be easily introduced by assuming a Young's modulus of the form Y1 = YR1 + jYI1, and a dielectric constant of the form [[epsilon]]3 = [[epsilon]]R3 + j[[epsilon]]I3.

7.0 Bibliography

1. Uchino, K.," Piezoelectric Ultrasonic Motors." Smart Actuator Symposium, 1994, ICAT, Penn State October 27, 1994, Course Notes.

2. Miu, D. "Mechatronics - Electromechanics and Contromechanics," 1993, Springer-Verlag.

3. Ikeda, T. "Fundamentals of Piezoelectricity," 1984, Oxford University Press.

4. Ueha, S. And Tomikawa, Y., "Ultrasonic Motors - Theory and Applications," 1993, Oxford University Press.

5. Auld, B. A., "Acoustic Fields and Waves in Solids - Volume I," 1990 2nd Ed., Krieger.